1.3.12 卡方分布
卡方(χN2)分布(N自由度)是N个具有标准正态分布(μ=0,σ=1)的随机变量的平方和的概率分布。图15示出了不同N值下的卡方分布PDF的例子。当N→∞时卡方分布收敛到正态分布。对于卡方分布,均值μ=N,方差σ2=2N。
卡方分布的PDF的公式是
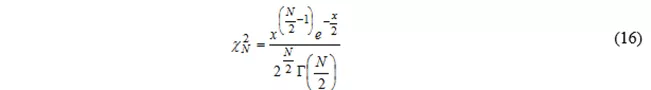
其中,Γ是伽玛函数。
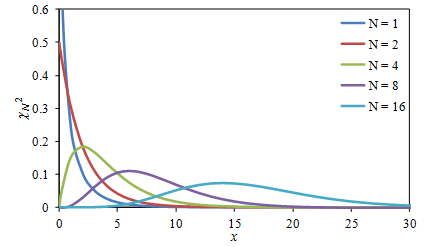
图14.N个平方值之和的卡方分布
因而用于计算均方的平方值都是卡方分布。如图15所示,使用了图2所示的轿厢的振动信号。如图,分布严重偏向小值,如χ12的简化公式所示。
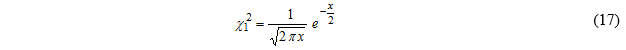
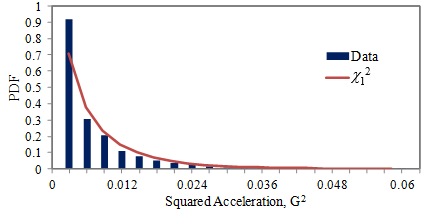
图15.图2的汽车振动数据的平方的PDF与χ12比较
由于方差σ2可从均方值确定(式3),σ2的置信区间可以用卡方分布确定。对于标准差σX的随机变量x,N个平方值的和具有σX2χN2分布,所以方差具有σX2χN2/N分布。由于χN2分布不对称,方差估计的置信区间不对称。如图16所示,给出了不同置信水平下N/χN2与N的关系。将方差的置信区间表示为区间:

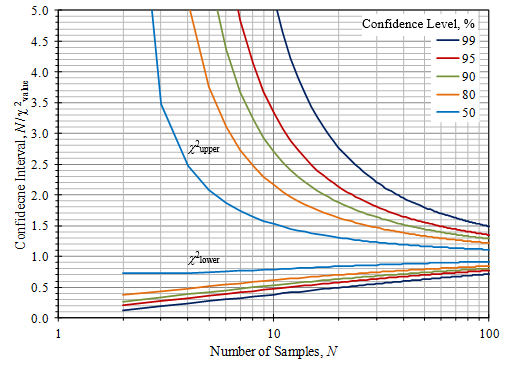
图16.使用小样本量的卡方分布的置信区间
对于N>100的情况,可以使用正态分布。方差估计的标准差为,可以使用图13的(对称)置信区间。
1.3.13 回归分析与最小二乘法
在非数学术语中,回归分析涉及将分散数据拟合为平滑曲线的技术。大约在1800年左右,为计算行星和彗星轨道确定执行此操作的“最佳”方法是发展正态分布[1]、中心极限定理[2]和最小二乘法[5]的主要动力。如今,回归分析仍用于重要数据的分析(例如,图18)。
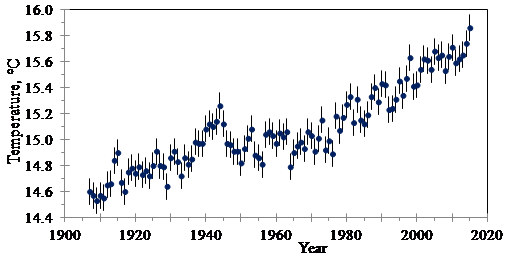
图18
如图18所示,最简单形式的线性回归将一系列数据点(xn,yn),n=1,…,N拟合为一条直线。直线的方程式是y=ax+b,其中a和b待定。误差或残差是每个xn处直线和数据点之间的差:en=yn–a xn–b。最小二乘法用于确定a和b的“最佳”值。这是通过对残差en的平方求和并找到使该和最小的a和b的值来完成的。(使用微积分:令“和”对a和b的导数趋向于零,并从这两个方程求出a和b。)所得公式为:
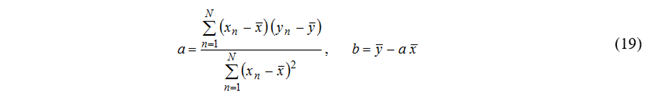
其中
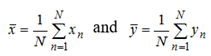
为均值。
可以通过假设误差为正态分布来获得此曲线拟合的置信区间。残差的方差为
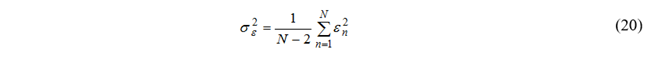
其中分母为N–2,因为a和b的两个方程使自由度减少了2。为此,必须添加确定的yn 数据的方差,σYN2。(通常假定测量误差为2σÝ,基于95%的置信水平)。直线的数值y的标准差,是
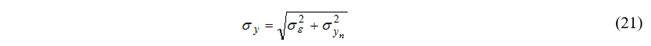
回归分析的“拟合优度”的常用度量是R平方(R-square)系数:
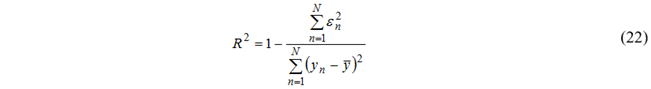
R2的平方根通常被称为相关系数,
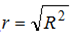
。在图18中,给出全球表面温度的例子σë=0.133ºC。每个温度测量中的误差范围被给定为±0.1ºC,所以假定σyn=0.050ºC。σÿ=0.14ºC和95%置信区间是±0.28ºC。R-square的计算值是R2=0.83。
在许多情况下,使用线性尺度时,数据无法很好地拟合为直线。与其尝试使用非线性曲线拟合,不如使用“对数”值进行线性回归通常很方便。例如log(y)-x、y-log(x)或log(y)-log(x)。用下例作为说明。在一个结构中的阻尼使冲击后振动的理论衰减速率为其中f是以Hz为单位的频率,t是时间(以秒为单位),ζ是临界阻尼比)。因此,为了确定阻尼值,在结构受到冲击后,测量均方根加速度水平与时间的关系,如图19a中所示,f=200Hz。当使用log(A)=log(Ao)-[2πfζlog(e)]t时,该理论衰减曲线绘制出来应该是直线,如图19b中所示。在这个例子中线性回归给出,斜率为-8.28,所以ζ=8.28/[2π f log(e)]=0.015。
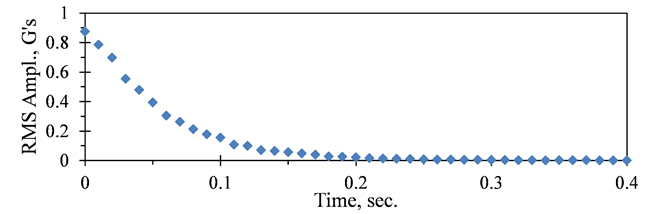
图19a.
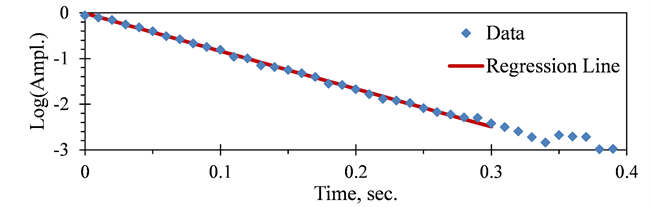
图19b.瞬态振动衰减的回归分析
1.3.14 瑞利分布

瑞利勋爵(Lord Rayleigh),1842-1919(约翰·W·斯特鲁特(John W.Strutt))
随机振动中,瑞利分布发生在若干种情况下。随机激励下的共振响应的峰值表现为瑞利分布。复杂系统中空间振动模式的振幅具有瑞利分布。第二种情况导致约翰·斯特鲁特(John W.Strutt)得出了以他名字命名的概率分布公式。他认为振动振幅是一个向量r,其a、b分量为遵从零均值、方差为σÔ2的相互独立的正态分布,如图所示:
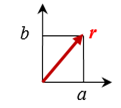
r的归一化大小由下式给出:
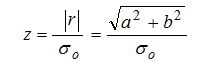
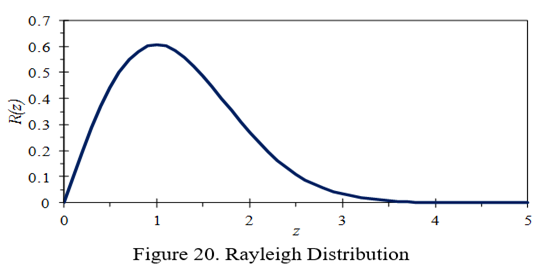
PDF由式23给出,如图20所示。
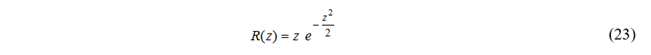
瑞利分布的PDF是不对称的,并且其均值不等于1而是≅1.25σo,σr≅0.655σo。
作为对此的说明,图21示出了悬臂梁振子的尖端对基部处的随机激励的振动响应。图22显示了峰值|Ai|(与梁中的峰值应力成比例)的直方图与瑞利分布的对比。该结果用于疲劳分析(请参见第3.3节)。
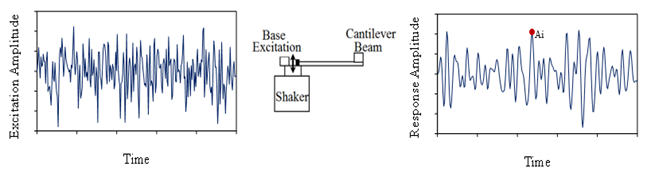
图21.悬臂梁基部激励的随机振动响应。
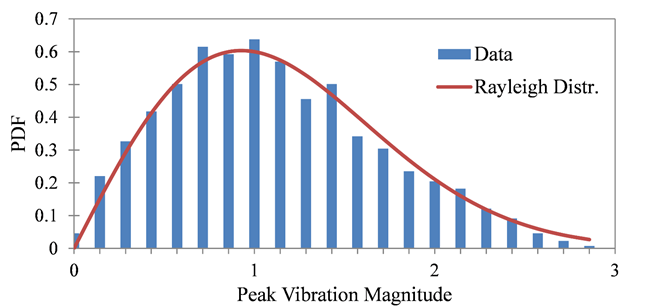
图22.峰值振动响应|Ai|的PDF
瑞利分布与χ22分布密切相关,因为瑞利变量都是χ22变量的平方根:
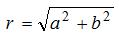
下图的面积P给出了估算峰值水平“不超过”的置信水平,并在图23中绘制为偏离均值的标准差数的函数。
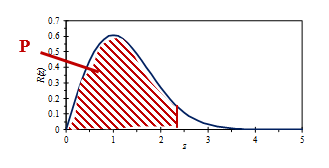
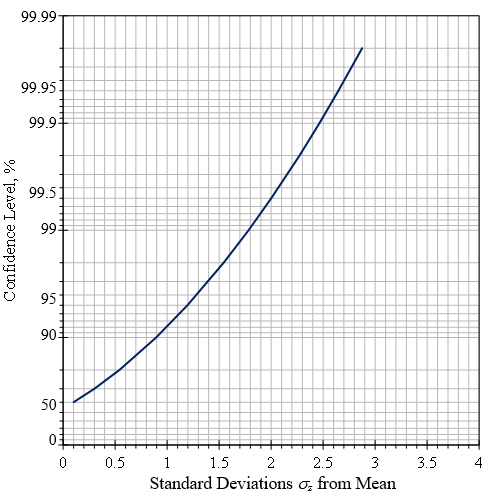
图23.具有瑞利分布的“不超过水平”的置信区间
1.3.15 对数正态分布
许多物理现象表现出对数正态分布。当系统的响应值由多个独立参数的乘积得出时,响应值的分布将趋于对数正态。这是因为乘积的对数是因子项的对数的和,而中心极限定理意味着值的对数将具有正态分布。例如,如果x=A·B/C,则log(x)=log(A)+log(B)–log(C),A、B、C为正值。图24显示了以线性和log x标尺绘制的对数正态分布。
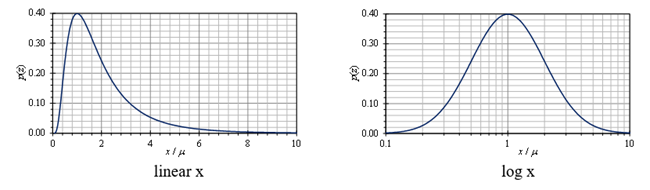
图24.对数正态分布
在随机振动中,这适用于整体随机条件下的振动大小分布。这在图25中用在名义相同的条件下运行的40部名义相同的柴油机的联轴器壳体的垂直和横向方向上测得的RMS加速度水平(ARMS)直方图的图表进行了说明。以分贝标度[分贝电平=20Log(ARMS/1μG),dB]绘制的测量数据与Log水平的正态分布进行比较,平均值为114.2dB,σ=3.5dB。
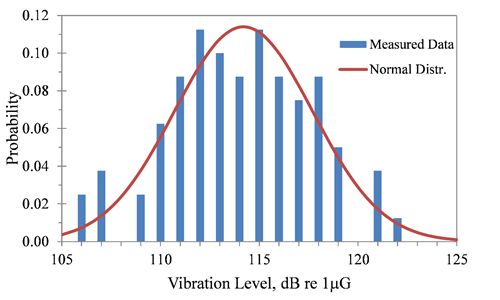
图25.发动机振动水平的分布

欢迎您关注VR公众号!
