1.3.9 正态(高斯)分布
统计分析中最常见且使用最广泛的概率分布是正态(或高斯)分布函数(有时称为“钟形曲线”)。PDF,即p(x),由式9定义,其标准形式示于图6,其中μ是均值,σ是变量x的标准差。作为对称分布,偏度=0,而峭度=3(超峰度=0)。

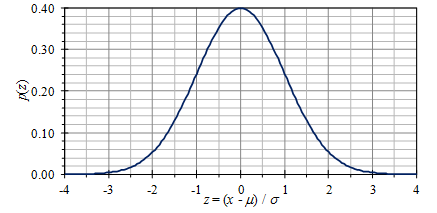
图6.正态(高斯)分布的PDF(“钟形曲线”)

卡尔·弗里德里希·高斯(Carl Friedrich Gauss),1777-1855
它以德国数学家卡尔·弗里德里希·高斯(Carl Friedrich Gauss)的名字命名,他在1809年关于行星和彗星的运动的文章中就得出了基本形式。他发现,通过使用函数 e^kδ2代表测量过程中随机误差δ的分布,(其中k是比例因子),他可以证明最小二乘法拟合数据的方法(见2.5节),提供了最好的(最有可能)的结果。他还使用它来确定一系列具有此类随机误差的测量值的均值的统计量(请参阅有关置信区间的课程)。
表示概率分布的另一种形式是累积分布函数(CDF),该函数绘制x小于特定值X的概率,该值通常写为P(x<X)。对于正态分布的情况绘制如图7所示。数学上它是由

其中erf(…)是误差函数。
在图形上显示为区域P:
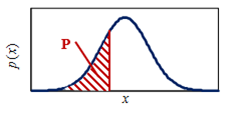
(根据定义,PDF曲线下的总面积等于1。)

图7.正态累积分布函数
正态分布完全由平均值和标准差定义,如式9中所示。因此,在许多情况下,这些值是使用式1和4从数据集中计算得出的,并假设为正态分布。如果在计算中使用分布的尾部(距平均值±2σ以外的水平)而没有首先检查数据的偏度和峰度是否与正态分布匹配,则可能导致严重错误。一个例子就是图3所示的湍流压力。
绘制CDF的另一种形式是将垂直轴比例转换为会产生正态分布的直线的比例。这称为正态概率图。这样可以更直观地确定数据是否为正态分布。在以前,用手将东西绘制在方格纸上时,有一种标准形式称为“概率方格纸”(见图8)。由于大多数计算机制图程序不具备此功能,因此可以通过将CDF值映射回法线Z值并绘制这些值与实际Z值的关系来构建类似的图。

图8.概率方格纸
在图9中使用来自图1和3的汽车振动和湍流压力数据显示了正态概率图的示例。直线对角线代表正态分布。汽车振动数据紧随其后,而湍流压力数据在分布的两端明显偏离。

图9. 来自图1和3的测量数据的正态概率图
1.3.10 中心极限定理
中心极限定理指出,随着N的增加,N个随机变量集合的总和(或平均值)将趋于具有正态分布。法国数学家拉普拉斯(Laplace)在1810年的许多一般情况下证明了这一点[2]。拉普拉斯还推导了一组随机数的平均值的标准差的表达式,从而证实了高斯推导正态分布时所设定的假设(在“置信区间”课程中对此进行了更多介绍)。

皮埃尔·西蒙·拉普拉斯(Pierre-Simon Laplace),1749-1827
中心极限定理最简单,最引人注目的例子是抛硬币。如果“真”硬币被抛N次,出现q个正面的概率由下式给出(称为二项分布)。
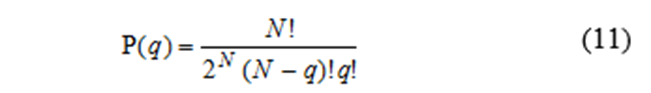
图10绘制了6次抛硬币的直方图,并与正态分布相对比。即使只有6次抛掷,这两个分布之间也有很好的一致性(尽管正态分布的尾部超出了q的可能值)。法国数学家棣莫弗在1733年已经注意到这个一致性,并使用(2/πN)1/2 e^ (2/N)(q–N /2)2作为大N下的式11的繁琐计算的近似值。但是他没有将其推广到其他情况。

图10.6次抛硬币中出现q次正面的概率
另一个示例是均匀分布在-0.5和0.5(可能是测量的不确定度范围)之间的随机变量x的平均值。通过对取这些随机变量的2个、3个和4个进行平均,可以看出逐渐收敛为正态分布,如图11所示。

图11.均匀分布随机变量均值的PDF
当PDF的大小以线性比例绘制时,尚不清楚分布尾部发生了什么。可以通过在对数刻度上绘制其大小来进行校正,因此可以在分布的尾部看到4个均匀分布的随机变量的平均值与正态分布之间的较大百分比偏差。在信号的极值对于了解被测产品的行为至关重要的情况下(一个例子是疲劳分析),这非常重要。
1.3.11 置信区间
在计算随机变量的点估计(例如均值)时,可以确定估计中可能的误差。这可以通过计算与置信水平相关的置信区间来完成。重要的是要了解置信区间和置信水平是相对应的概念。较高的置信水平要求较大的置信区间。较低的置信水平允许较窄的置信区间。
在对独立随机变量求和时,均值和方差随着相加。例如,在对独立随机变量A和B求和时:
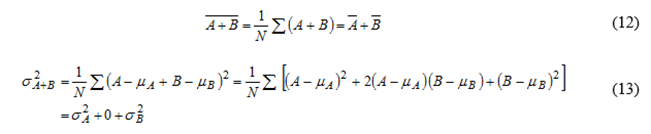
式13的结果可以用来确定已知标准差sx的N个随机变量x的均值的标准差。x的和的方差为Nsx2,因此标准差为sx。除以N以计算均值的标准差,得出

假设x为正态分布,则此结果用于确定估计均值的置信区间。重要的是要意识到置信区间取决于该区间的概率或置信水平。它通过计算从真均值μ偏离一定倍数的标准差的范围内的概率来确定,如图区域P所示。

置信水平P作为(从真均值μ偏离标准差的数量)的函数绘制在图12中。因此,±1的置信区间具有68%的置信水平。(95%的置信区间为±2,99.7%的置信区间为±3,等)
[从式14注意到当N→∞时→。]

图12.估计均值的置信水平与置信区间
基于中心极限定理,几乎总是采用正态分布来估计均值。使用上一节中从四个值的平均值获得的平均值的示例,(-0.5,0.5)均匀分布的标准差为0.144。假设为正态分布,则95%的置信区间为±0.288。在实际上,95%的置信区间取为0.24。
当从较小的数据样本中获得均值和标准差时,置信区间的确定会更加复杂。在这种情况下,通常会使用t分布,因为样本分布的不确定性增加,因此对于相同的置信水平,它会给出较大的置信区间。对于N>3个样本,与使用等式13相比,样本均值的方差以(N–1)/(N–3)的比率增加。图13示出了用于不同置信度水平的置信区间的标准差修改后的数值(tvalue),它是样本数的函数。那么对真实均值的估计是

对于N>50的情况,t分布收敛到正态分布,图13可以使用。

图13.使用小样本量的t分布的置信区间
值得注意的是,在置信区间的表述中通常会省略置信水平。在许多情况下,假定置信水平为95%,并使用大约±2σ的置信区间。许多民意测验在给定的百分比结果后附加±%的误差范围,这些情况都是这种含义。在有N个受访者的调查中,标准差被假定为σ=0.5/N1/2,因此±4%的误差范围(置信度为95%)仅意味着大约N=1/(0.04)2=625人被调查。(4%=0.04=2σ=1/N1/2)

欢迎您关注VR公众号!
